任意波發(fā)生器是越來(lái)越重要��、應(yīng)用越來(lái)越廣的一種信號(hào)源��。拿到一個(gè)高性能任意波發(fā)生器的技術(shù)手冊(cè)��,很多工程師會(huì)發(fā)現(xiàn)����,越來(lái)越難看懂和理解任意波發(fā)生器的相關(guān)技術(shù)指標(biāo)和功能特點(diǎn),比如:什么是真任意波(True arb)�����?什么叫插值DAC(interpolating DAC)���?什么叫去毛刺DAC(Deglitching DAC)和分布式重采樣(Distributed Resampling)���?什么是Doublet Mode?什么是數(shù)字上變頻�����?什么是動(dòng)態(tài)序列(Dynamic Sequencing)�?什么是流盤(pán)播放(Streaming)?等等。為此����,這篇文章基于“Agilent Fundamentals of Arbitrary Waveform-A High Performance AWG Primer”參考手冊(cè),介紹現(xiàn)代任意波發(fā)生器所涉及的相關(guān)的基礎(chǔ)知識(shí)��。
本文引用地址:http://2s4d.com/article/201701/336010.htm1 AWG采樣理論
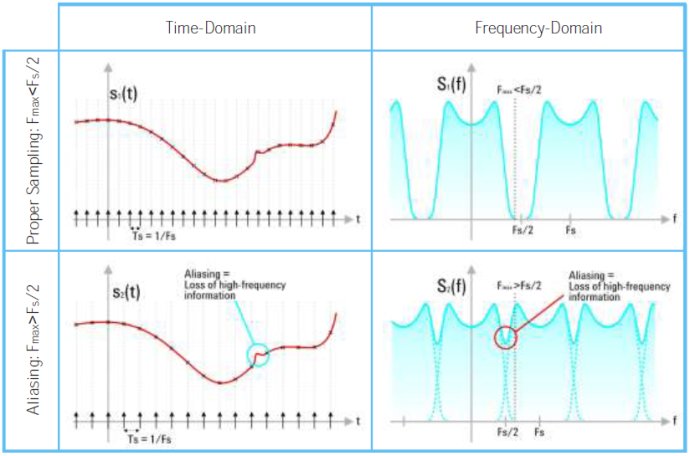
圖1 奈奎斯特采樣理論
DAC和ADC一樣�����,也需要滿足奈奎斯特采樣定理,即轉(zhuǎn)換速率(采樣速率)需要滿足:
Fs>2 x Fmax
Fs是轉(zhuǎn)換速率/采樣速率�����;
Fmax是產(chǎn)生目標(biāo)信號(hào)的最高頻率分量�。
如果不能滿足奈奎斯特定理,會(huì)導(dǎo)致頻率混疊���,會(huì)丟失想產(chǎn)生信號(hào)的高頻信息���。
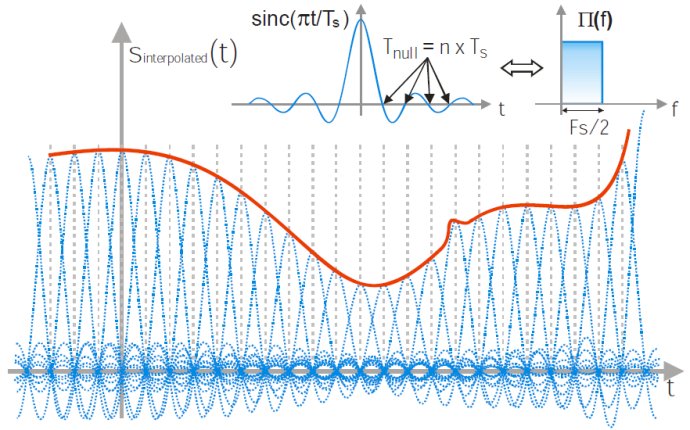
圖2 帶限信號(hào)的波形重建
用一個(gè)理想的奈奎斯特濾波器進(jìn)行濾波,可完整重建數(shù)字形式域的信號(hào)波形����,相當(dāng)于在實(shí)際采樣點(diǎn)之間進(jìn)行插值,插值后的信號(hào)經(jīng)過(guò)DAC轉(zhuǎn)換后�����,可完整重建模擬信號(hào)����。理想奈奎斯特濾波器的頻域特性是帶寬為Fs/2的磚墻低通濾波器�����;時(shí)域特性是Sinc函數(shù)。
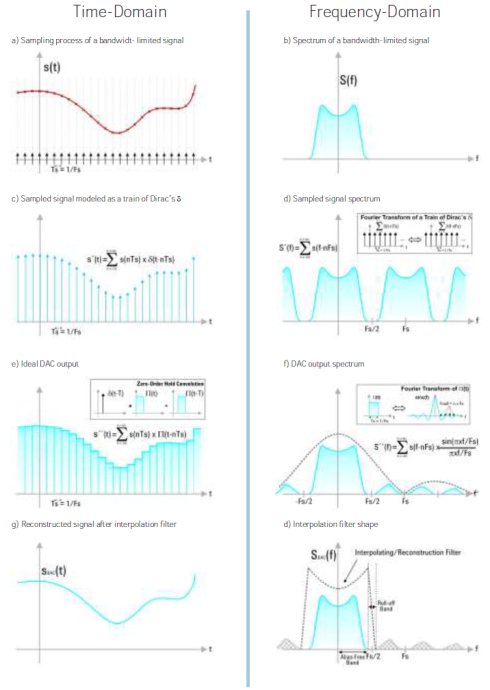
圖3 理想任意波發(fā)生器的信號(hào)處理過(guò)程(時(shí)域和頻域?qū)?yīng))
上面這些圖從時(shí)域和頻域角度展示了DAC轉(zhuǎn)換前后波形的特征��。對(duì)于一個(gè)帶限信號(hào)��,純數(shù)字化的信號(hào)的頻譜是周期拓展的���,但是理想DAC實(shí)際輸出的波形的頻譜卻不是周期拓展的���。因?yàn)閿?shù)字化的信號(hào)相當(dāng)于與一脈寬為1/Fs的脈沖進(jìn)行了時(shí)域卷積,在頻域中相當(dāng)于與一個(gè)Sinc函數(shù)進(jìn)行了乘積運(yùn)算���,所以會(huì)有許多旁瓣產(chǎn)生���。可以采用內(nèi)插的方式在數(shù)字域里濾除拓展的頻譜�����,也可以采用比較好的模擬濾波器在模擬域里濾除拓展的頻譜���,或者采用組合的方式進(jìn)行濾除����。剛好滿足奈奎斯特采樣定理的波形重建實(shí)際上是比較困難的。
2 AWG架構(gòu)
下面分析常見(jiàn)的幾種AWG架構(gòu)���。
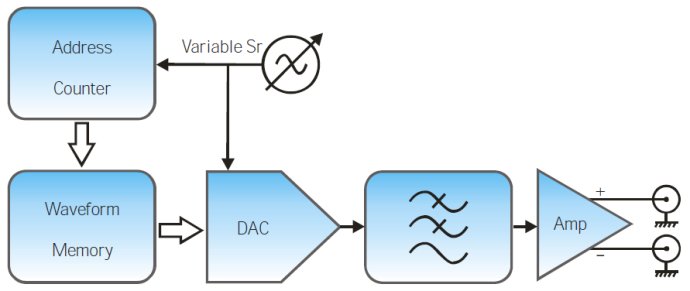
圖4 真任意波(true-arb)架構(gòu)AWG框圖
真任意波架構(gòu)如上圖所示����,樣本被一個(gè)接著一個(gè)從內(nèi)存中讀取��,DAC把它們轉(zhuǎn)換成模擬信號(hào)����,使用使用者設(shè)置的固定采樣速率。內(nèi)存的數(shù)據(jù)讀取速度由采樣率決定�����,內(nèi)存的數(shù)據(jù)被順序地讀取�。
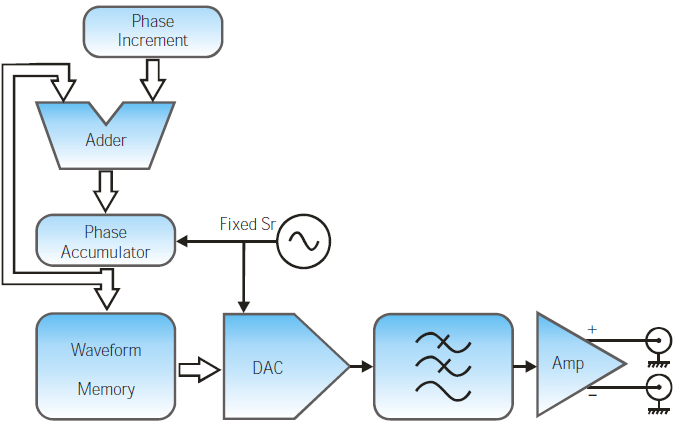
圖5 直接數(shù)字合成(DDS)架構(gòu)AWG框圖
直接數(shù)字合成即DDS架構(gòu)如上圖所示,這里DAC工作在固定的采樣速率����,使用者控制存儲(chǔ)在內(nèi)存里的波形的重復(fù)速率。對(duì)于每個(gè)DAC的時(shí)鐘周期���,通過(guò)改變相位累加器的相位值��,去確定內(nèi)存的接入地址�。內(nèi)存數(shù)據(jù)不需要順序讀出�����。這種架構(gòu)允許無(wú)縫改變存儲(chǔ)在內(nèi)存中波形的重復(fù)頻率����,允許直接頻率掃描或PM/FM調(diào)制信號(hào)的產(chǎn)生。因?yàn)檫@個(gè)原因��,DDS成為流行的函數(shù)發(fā)生器和低端任意波發(fā)生器的常用架構(gòu)�����。
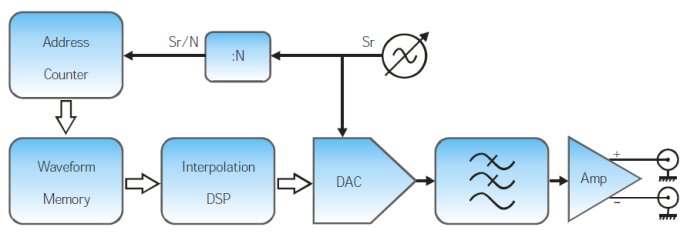
圖6 內(nèi)插DAC(Interpolating DAC)架構(gòu)AWG框圖
內(nèi)存DAC的架構(gòu)要求DAC的采樣率很高���,高于內(nèi)存的讀取速率���。內(nèi)插DAC架構(gòu)是在波形讀取器件和DAC器件之間增加一個(gè)內(nèi)插DSP處理器,內(nèi)插函數(shù)可以是線性內(nèi)插,或FIR低通濾波器內(nèi)插���。這種架構(gòu)的益處是不需要太快的內(nèi)存接入速度��,可以達(dá)到高品質(zhì)信號(hào)質(zhì)量��。但是最大頻率分量仍然受限于內(nèi)存接入速度��,而不是DAC采樣速率��。
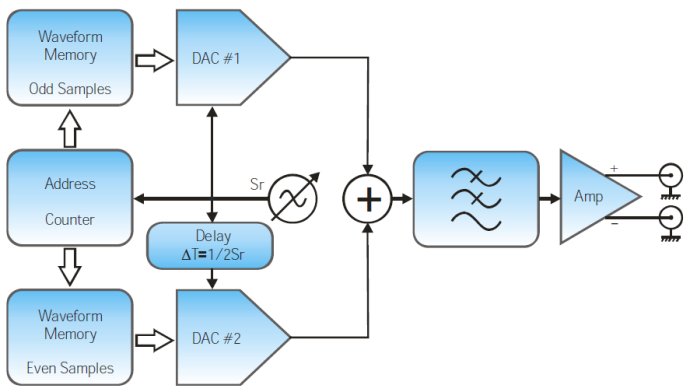
圖7 偽內(nèi)插DAC(pseudo-interleaving DAC)架構(gòu)AWG框圖
偽內(nèi)存AWG架構(gòu)通過(guò)組合兩通道AWG或2個(gè)DAC,實(shí)現(xiàn)等效采樣率加倍的目的�。兩通道間的時(shí)差必須是采樣周期的一半����;樣點(diǎn)分成奇數(shù)點(diǎn)和偶數(shù)點(diǎn),分別存在各個(gè)通道中���。這種技術(shù)有效地?cái)U(kuò)展了可用的頻率范圍��,也能夠提升每個(gè)DAC的信噪比(由于兩個(gè)通道的DAC的噪聲是不相參的)��,但是信號(hào)品質(zhì)對(duì)時(shí)序精度和通道頻響失配都非常敏感�����。
3DDS和True Arb對(duì)比

圖8 DDS架構(gòu)AWG���,兩種不同的存儲(chǔ)設(shè)置�����,產(chǎn)生一個(gè)三角波
上圖是用兩種不同波形內(nèi)存設(shè)置來(lái)產(chǎn)生一個(gè)三角波。a的時(shí)間分辨率低于b���。時(shí)間間隔誤差TIE圖表明較高分辨率波形具有較低的失真�,雖然輸出的采樣速率是一樣的�����。
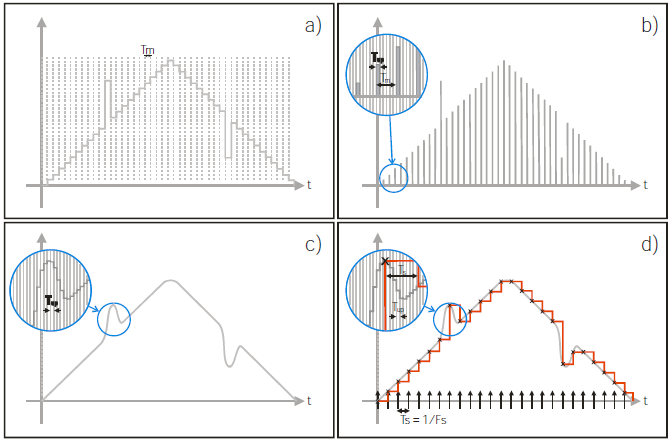
圖9 True Arb的快信號(hào)處理過(guò)程
上圖是真任意波AWG的信號(hào)處理過(guò)程��。存儲(chǔ)在內(nèi)存里的原始信號(hào)是較高采樣率的����,內(nèi)插低通濾波器增加點(diǎn)的密度(也可以直接存儲(chǔ)更高采樣率的波形),DAC輸出的波形產(chǎn)生帶快信號(hào)的模擬信號(hào)����。
4DAC量化噪聲
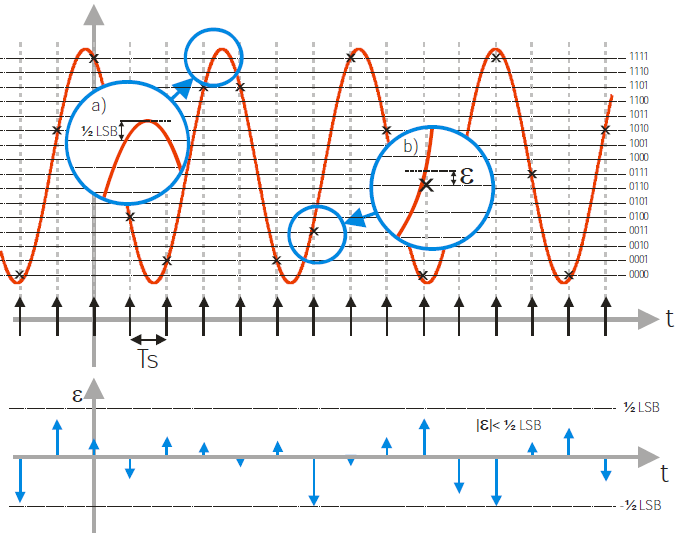
圖10 在被采樣的波形上分析量化噪聲
量化噪聲能夠作為采樣波形自身進(jìn)行分析�����。量化噪聲波形的上下邊界是+-1/2LSB,時(shí)間上與波形一致���。輸人波形的幅度可能超越1/2 LSB(a),仍然保持邊界錯(cuò)誤條件(b)。
只考慮量化噪聲的信噪比SNR或SQNR(信號(hào)到量化噪聲比)公式:
SNR(dB)=6.02N+1.76dB+10log10(Fs/2B)
B是帶寬�����。
過(guò)采樣DAC能夠提升信號(hào)到量化噪聲比���。理論上的分辨率提升(以位數(shù)表示)可由下面公式得到:
提升位數(shù)=10log10(過(guò)采樣因子)/6.02
這意味著��,對(duì)于非內(nèi)插DAC,采樣率增加到4倍���,等效于提升1位分辨率。
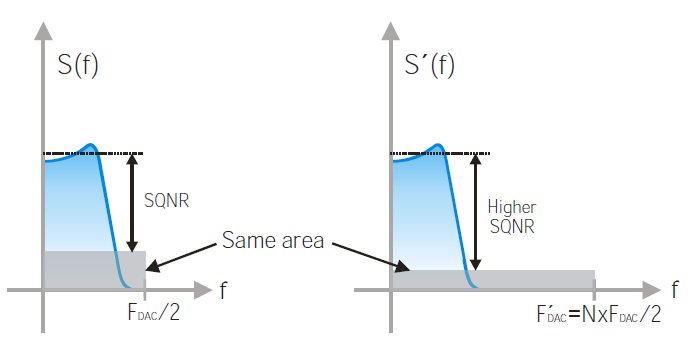
圖11 量化噪聲在完整奈奎斯特帶寬上的拓展
量化噪聲拓展到完整的奈奎斯特帶寬��。對(duì)于一個(gè)帶限信號(hào)�����,通過(guò)增加采樣率可以減少噪聲功率譜密度�,由于同樣的功率被分配到更大的帶寬上����。這種效果可被內(nèi)插DAC架構(gòu)的AWG利用�����。






















評(píng)論